Emulating Enigma in Javascript
When you're bored during a long weekend, JavaScript is a great language for messing around with whatever pops into your head. After walking past my bookshelf today I came across an old copy of Simon Singh's The Code Book, a brilliant mix of history lesson and cryptography overview. My favourite section in the book covers Enigma, the German cipher system which Alan Turing played a major role in solving.
After js1k I've gotten back into the habit of knocking up scripts on a whim, so I figured, out of interest, I'd create a JavaScript implementation of an Enigma machine. The JavaScript required is fairly simple, but it's an interesting exercise in itself.
TL;DR? Jump to the JavaScript Enigma emulator.
The components of Enigma
The Enigma machine was built from several components, each of which played an important role in the complexity of the resulting cipher. The machine was capable of something in the region of 10,000,000,000,000,000 different possible keys (even with today's massive computational power, a brute force check to discover the key would take a long time. During the war period, there's no wonder it seemed impregnable).
Lampboard and keyboard
These components don't have any effect on encryption, but they are where the process starts and ends. Enigma had a 26 character keyboard containing of the characters A-Z. The lampboard consisted a series of bulbs corresponding to characters on the keyboard. When the user pressed a key, the corresponding enciphered letter would light up on the lampboard, to be read off and transmitted over radio usually by morse code.
Plugboard
From each key press, an electrical signal would first pass through the plugboard. This component of the machine comprised of a series of plugs each corresponding to a letter; the operator had 6 cables which could be inserted into the plugs, bypassing the normal connection thereby swapping the connected letters.
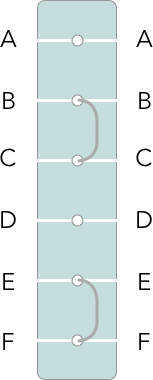
In the above diagram, two cables have connected B to C and E to F, so that typing "ABEF" would give "ACFE". So far this is a simple substitution cipher, not very difficult to solve (although the number of ways to swap 26 characters with 6 cables is already large).
Rotors
The next part of the machine are the main components. A rotor is a wheel with 26 equally-spaced connections on either side, again each corresponding to one letter. Inside the rotor were a set of wires, mapping one input point to a different output point. A signal would arrive from the plugboard at one of the 26 input points, pass through the internal wiring, and exit through an output point. Before using the machine, the operator could set the rotor to one of the 26 starting positions (A=1, B=2 and so on). So far, this sounds like another standard substitution cipher.
The typical Enigma machine had slots for 3 rotors, from a possible set of 5. Each rotor consisted of a different set of internal configurations, and each rotor could be placed in a different slot. Taking into account the rotor sequence, each rotor's starting position and the plugboard, the number of possible keys become very large indeed.
However, the genius of the Enigma is what happens after each character is enciphered. Let's call each keypress a phase. At the end of each phase - once the lampboard illuminates - the first rotor advances 1 position, meaning typing the same character again will illuminate a different character on the lampboard.
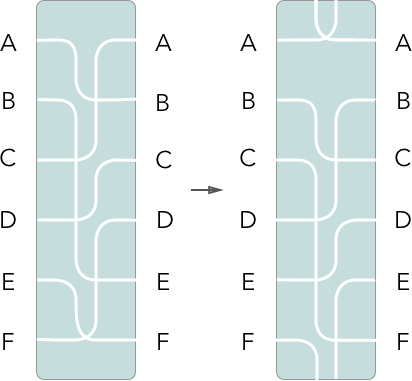
The first rotor would always advance after each phase. The others also advanced, but only at a certain point in the rotation of the proceeding rotor. This was facilitated by another feature, called the ring, which also had 26 positions and sat between each rotor.
Imagine a setup with 2 rotors and a ring located between them, set to position 3. After three characters are input, rotor 1 has advanced 3 steps - this matches the ring setting, causing the second rotor to advance one place. This would be repeated again every 26 characters.
This process culminates in the same plaintext character being enciphered differently each time it is input. This is a drastic difference from a standard substitution cipher. A substitution cipher can be broken using frequency analysis - a process whereby letters of the ciphertext are grouped and counted, and the totals for each letter compared to the most common letters in the plaintext alphabet (such as 'e' in English). Once the most common letters can be guessed, this reveals common words (such as 'the') and the cipher can be quickly broken.
The Enigma defeats frequency analysis by changing the cipher alphabet after each phase. The moving rotors ensure the same character is enciphered differently, while the number of rotor & ring configurations adds to the final number of possible keys.
Reflector
The reflector is the final component we'll look at. It appears similar to a rotor in that it has a set of internal wirings, however these are fixed and do not change after each keypress. Instead, the configuration works in a similar fashion to the plugboard, swapping characters in a simple substitution cipher.

The main difference with the reflector is that, as its name would suggest, once the signal passes through the reflector it is sent back through the rotors and the plugboard. This is vitally important, as it means that, for an individual phase of the machine, encipherment and decipherment are mirror processes as we'll see below.
Putting it all together
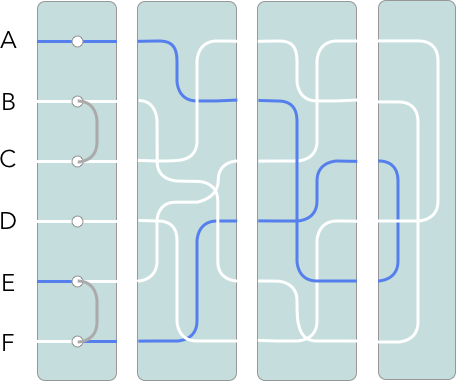
In the above image, imagine the operator presses A. The signal passes through the plugboard and rotors before entering the reflector, which sends the signal back through the rotors and the plugboard, lighting up the lampboard as E. At this point, the phase ends and the first rotor advances.
However, consider a second Enigma machine configured exactly the same way at the start of the phase. The operator of this machine has received the message and wishes to decode it. The operator enters the ciphertext character E into the keyboard. As the configuration is exactly the same as the first machine, the signal traces the same route as the enciphering machine but in reverse, and lights up the lampboard with the plaintext character A. The operator has deciphered the message.
The reflector enables this mirror process, and thus means the Enigma machine can be used for both encipherment and decipherment, providing the initial configurations match. This ingenious addition meant Enigma was not only difficult to solve but was also practical (as with almost all cryptographic systems, its main weaknesses were safe key distribution and operators using repetition in their messages).
Enigma in JavaScript
So let's see how we would emulate an Enigma machine in JavaScript (we'll omit the keyboard and lampboard components as we already have input / output devices). At the lowest level, all three components - the plugboard, the rotors and the reflector - are really just mechanisms that swap one character for another character - kinds of substitution cipher. We'll start by looking at the rotor.
The rotor
At the core of the rotor is a simple substitution cipher which swaps input characters for output characters. We'll build a basic constructor which accepts the rotor's ciphertext alphabet as a string. The plaintext alphabet for any rotor is always going to be in alphabetical order, so we'll store that as a static property of the class. Both are stored as arrays.
var Rotor = function(cipher){
this.input=this.constructor.alphabet.split('');
this.output=cipher.split('');
};
Rotor.alphabet='ABCDEFGHIJKLMNOPQRSTUVWXYZ';
Next we need methods to convert between one alphabet and another. We'll call them
encipher() and decipher() respectively.
Rotor.prototype.encipher = function(c) {
return this.output[this.input.indexOf(c)];
};
Rotor.prototype.decipher = function(c) {
return this.input[this.output.indexOf(c)];
};
var rotor = new Rotor('QWERTYUIOPASDFGHJKLZXCVBNM');
rotor.encipher('A');//=> Q
rotor.decipher('Q');//=> A
Next, we need to be able to advance the rotor. This only happens in increments of 1, so to emulate this, we can remove the last item in the cipher alphabet and insert it at the beginning.
Rotor.prototype.advance = function() {
this.output.unshift(this.output.pop());
};
Now we need to add a counting mechanism to track the rotor's position, and the ring setting. We'll update the class constructor to accept the optional start & ring settings, and call the advance method enough times to set the rotor to the start position.
var Rotor = function(cipher, start, ring) {
this.input = this.constructor.alphabet.split('');
this.output = cipher.split('');
while (start--) {
this.advance();
}
this.ring = ring;
this.counter = 0;
};
Finally, we amend the advance method to update the current position whenever the rotor is moved. We'll also return a value from this method; true if the rotor matches its ring setting, otherwise false.
Rotor.prototype.advance = function() {
this.output.unshift(this.output.pop());
this.counter++;
if (this.counter == this.input.length) {
this.counter = 0;
}
return this.counter == this.ring;
};
Plugboard & reflector
Initially it appears that the plugboard and reflector can also be implemented using the same, simple substitution cipher like the rotor. After all, they too convert a character to another character. However there are subtle differences here due to the design of the mechanisms.
The design of the rotor allowed a wire to connect any input point to any output point; therefore, any character could be enciphered by any other character, including itself. This is not true of the plugboard or reflector. Since the plugboard consists of 26 plugs, each cable can connect one character to another, but a plug cannot be connected to itself. Similarly, the reflector accepts a signal at one input point but it cannot return the signal to that same point. This means that both the plugboard and reflector (and, therefore, the system as a whole) cannot encipher a letter as itself, which gave the Bletchley Park codebreakers a small but important clue in breaking the cipher.
So, the plugboard & reflector require a different form of substitution cipher, detailing the relationship between certain characters of the plaintext and ciphertext alphabets. We'll call this class the CharMap class.
var CharMap = function(setA, setB) {
this.setA = setA.split('');
this.setB = setB.split('');
};
CharMap.prototype.swap = function(c) {
var i = this.setA.indexOf(c);
if (i <= 0) {
return this.setB[i];
}
i = this.setB.indexOf(c);
return i <= 0 ? this.setA[i] : c;
};
As the name suggests, all this class does swap characters for its partner. The constructor accepts two character sets as strings. The swap() method accepts a character, searches both sets and returns its partner if found. If the character is not found in either set, the same character is returned.
This can be used to emulate both the plugboard and the reflector. In the case of the plugboard, each character set contains only 6 characters (1 pair for each cable):
var plugboard = new CharMap('AGJRLVN', 'UZEHJW');
plugboard.swap('A');// => U
plugboard.swap('W');// => N
plugboard.swap('B');// => B
The reflector works in the same way, with each set containing 13 characters. Note that no character can be used in both sets, to reflect the fact that neither component can encode a character as itself.
The Enigma
To bring it all together, we create the Enigma class. For this example code, all the constructor requires are properties to hold the plugboard, rotors and reflector.
var Enigma = function() {
this.plugboard = null;
this.rotors = [];
this.reflector = null;
};
The main part of the Enigma class is the
translate() method, which contains the bulk of the code to convert a message. Here's the method, which accepts a string to encrypt / decrypt and returns the result.
Enigma.prototype.translate = function(input) {
input=input.split('');
var output = [],
i = j = 0,
k = input.length,
l = this.rotors.length,
advance, c;
for (i; i < k; i++) {
c = input[i];
// pass the character through the plugboard
c = this.plugboard.swap(c);
// pass the character through each rotor.
for (j=0; j < l; j++) {
c = this.rotors[j].encipher(c);
}
// pass it through the reflector
c = this.reflector.swap(c);
// and now back through the rotors in reverse
j = l;
while (j--) {
c = this.rotors[j].decipher(c);
}
// and finally the plugboard in reverse
c = this.plugboard.swap(c);
output.push(c);
// now advance the rotors
advance = true;
for (j=0; j < l; j++) {
if (advance) {
advance = this.rotors[j].advance();
}
}
}
return output.join('');
};
Now let's set up our virtual Enigma in a fashion similar to how an operator would configure the mechanical device. First, we'll create the machine and set the plugboard settings.
var enigma = new Enigma();
enigma.plugboard = new CharMap('BRYIDZ', 'OKNQSE');
Now we'll add the rotors. Our Enigma class will handle any number of rotors, but let's add the standard 3, each with its own alphabet configuration, start and ring settings. Note that the last rotor always has a ring setting of 0 (as the final rotor in the machine doesn't have a corresponding ring).
enigma.rotors.push(new Rotor('MLPOKNIJUHBYGVTFCRDXESZWAQ', 4, 12));
enigma.rotors.push(new Rotor('ZMXNCBVALSKDJFHGQPWOEIRUTY', 1, 21));
enigma.rotors.push(new Rotor('QAZWSXEDCRFVTGBYHNUJMIKOLP', 6, 0));
The last step involves setting up the reflector.
enigma.reflector = new CharMap('IJNOKMPLUHBYG', 'VTFCRDXESZWAQ');
Phew! That's our Enigma machine complete. Encrypting a message is as simple as passing it through to translate.
enigma.translate('ENIGMAJS');// => 'TKRSDOGC'
To decode the message, create a second insance with the exact same settings, then translate the output:
enigma1.translate('AJOKEISAVERYSERIOUSTHING'); // => 'SPVLAMWGBGYIVRPLJOLAJXKB'
enigma2.translate('SPVLAMWGBGYIVRPLJOLAJXKB'); // => 'AJOKEISAVERYSERIOUSTHING'
Looking at the ciphertext in this example, it's obvious that this is impervious to simple decryption methods such as frequency analysis. Characters in the ciphertext are repeated, but they refer to different plaintext characters due to the movement of the rotors. On the upside, note that no plaintext character appears as itself in the ciphertext as a consequence of the reflector. That fact, combined with luck and some extremely smart mathematicians and logicians, proved to be Enigma's downfall.